当塾では、オリジナルの教材を提供しております。(無料)
コンセプトは「自分の足で歩く」

当塾では、基本から参加し体験してもらいます。上の問題では数が多くなると、筋をまとめて式にするよう促します。
つるかめ算は難しいとされていますが、当塾ではすんなり受け入れる子が大半。
一斉授業、板書の説明は「動く歩道」 個性的な試行錯誤をするヒマがない。運んでもらうのは楽で、そうでなければ問題を解かなくなる。
当塾では、教えない算数の公式があります。
例えば、割合の三公式。
そんなものを教えてしまうと、くらべる量×割合だっけ? 元にする量÷割合って何だっけ?、などと混乱の元凶に。
割合がトンチンカンな子の共通点は、「元にする量」から筋を立てないこと。
当塾では、「元にする量」×割合=くらべる量、しか教えない。生徒は「元にする量」を第一に探し、問題が高度化してもスムーズ。
A〜Sレベルまで、この公式1つで何の問題もなくこなせる。「トン」の段階で混乱する芽を摘むので、後がスムーズ。
例えば、速さの三公式。
速さは、距離なのか時間なのか? トンチンカンな子は、この段階から間違う。
1分に進む距離とか、1時間に進む距離。当塾では、速さの意味しか教えない。意味が浸透すれば、式は自然に出てくる。
例えば、天秤図。大手塾ではさかんに教えているが、当塾では教えない。
2つの食塩水を混ぜる場合など、2量の平均を簡易的に出す方法。生徒は表面的な理解で当てはめる場合が多い。
3量となると、追いつかなくなり応用が効かない。面積図を横にすると天秤図、当塾では無視する解法です。
例えば、 円すいの側面積。母線×半径×3.14。当塾では教えない。教えなくても、習熟すると、ひとりでにそこに行き着く。
初めからこの公式を使う子に、意味を聞くと「だって公式だから」と言う子がほとんど。自分で歩かないクセがつく。
当塾で教えるのは、半径/母線、のみ。側面のおうぎ形の割合のみで、いろいろなアプローチの問題に対応できる。
解法を多く知ると、得した気分で喜ぶ。それは、経験の浅い素人の考え。
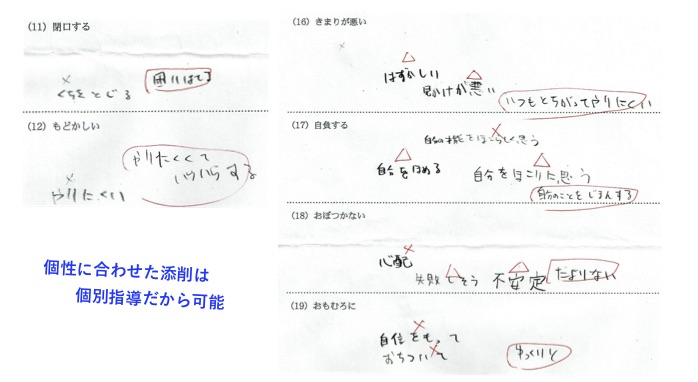
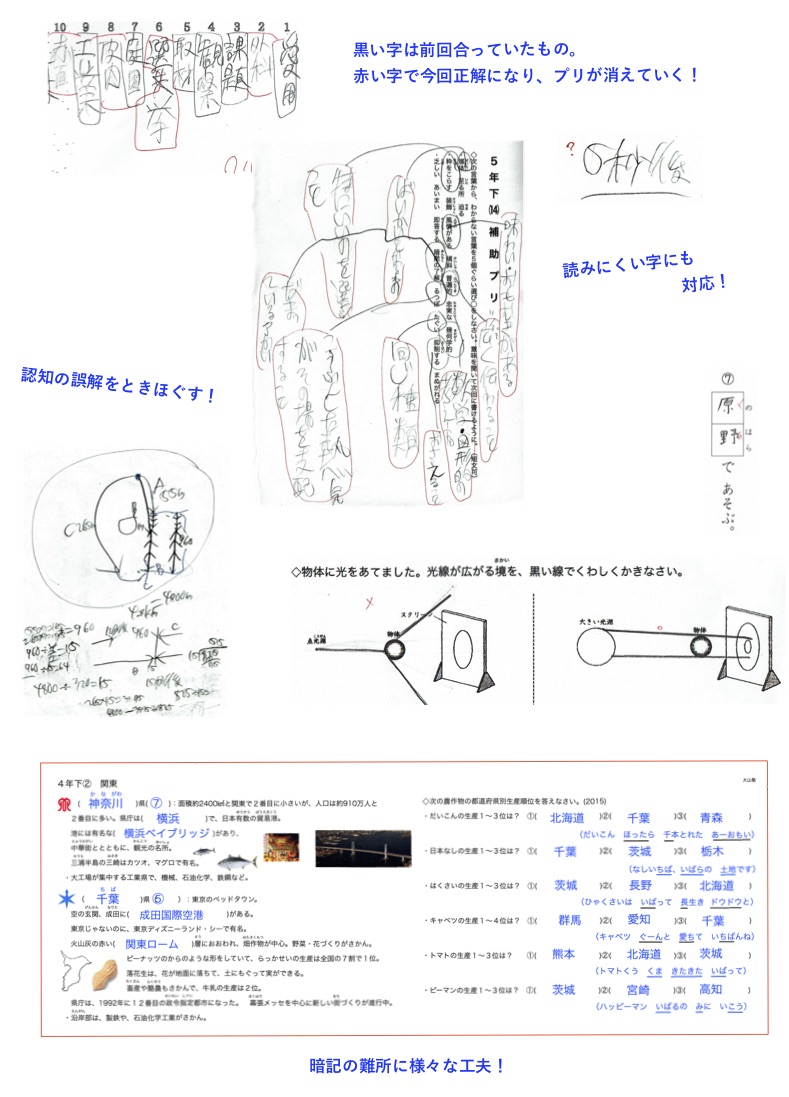
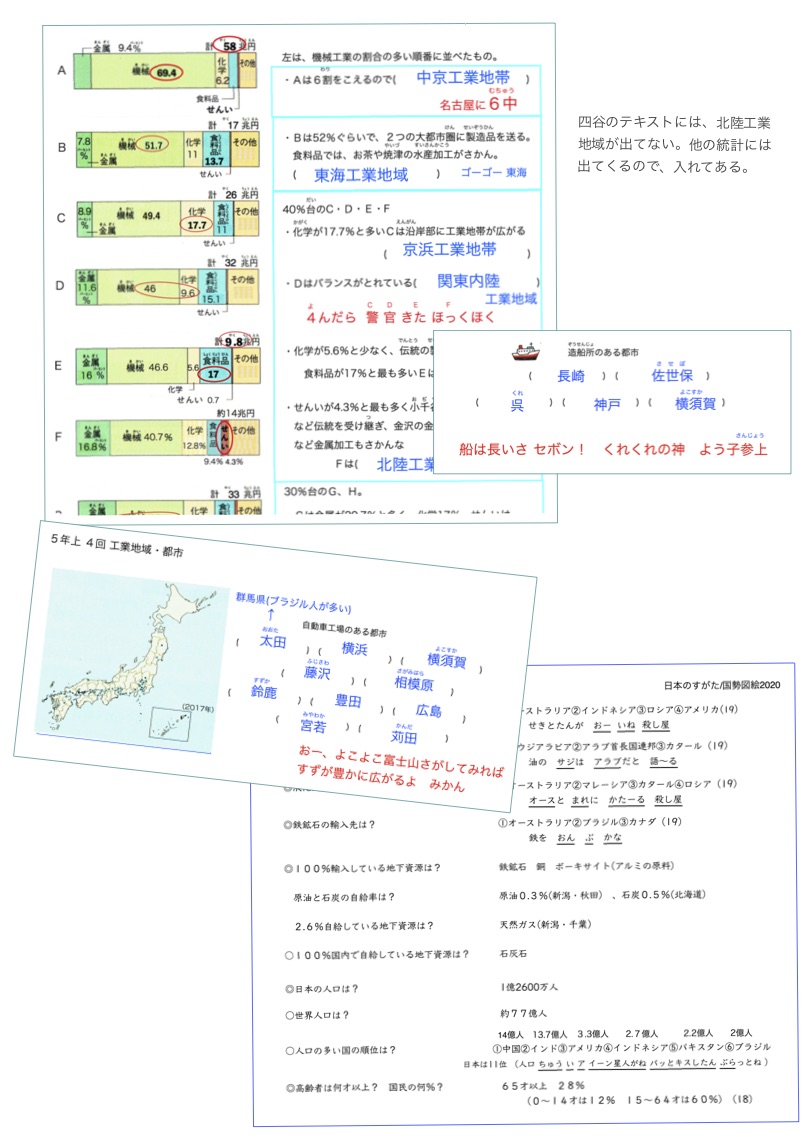

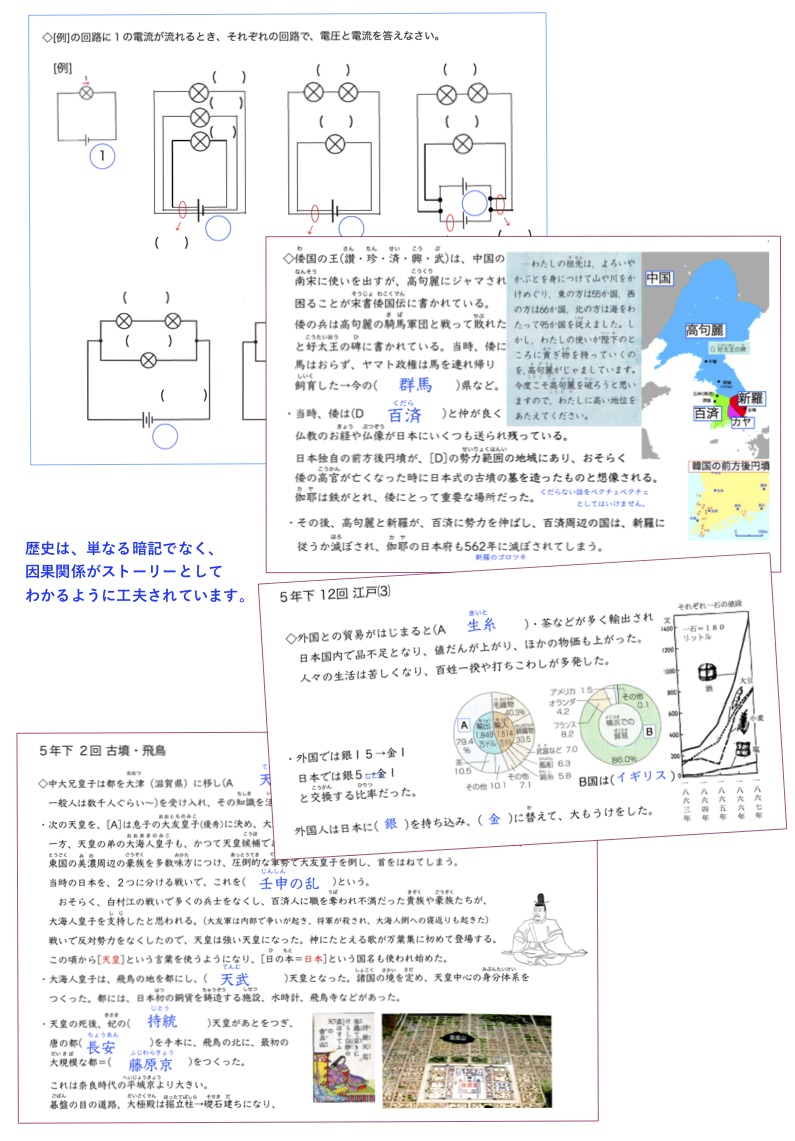





歴史は、ストーリーが見えるように作られています。
細かい部分は忘れてもいいので、時代の雰囲気が残れば良いかなと思います。
生徒は、穴埋めの答えだけを覚えることが多いと思われますが、ふと疑問をいだいた時に役立てば、と思います。
……………………………………………………………………………………………………………………………………………………………
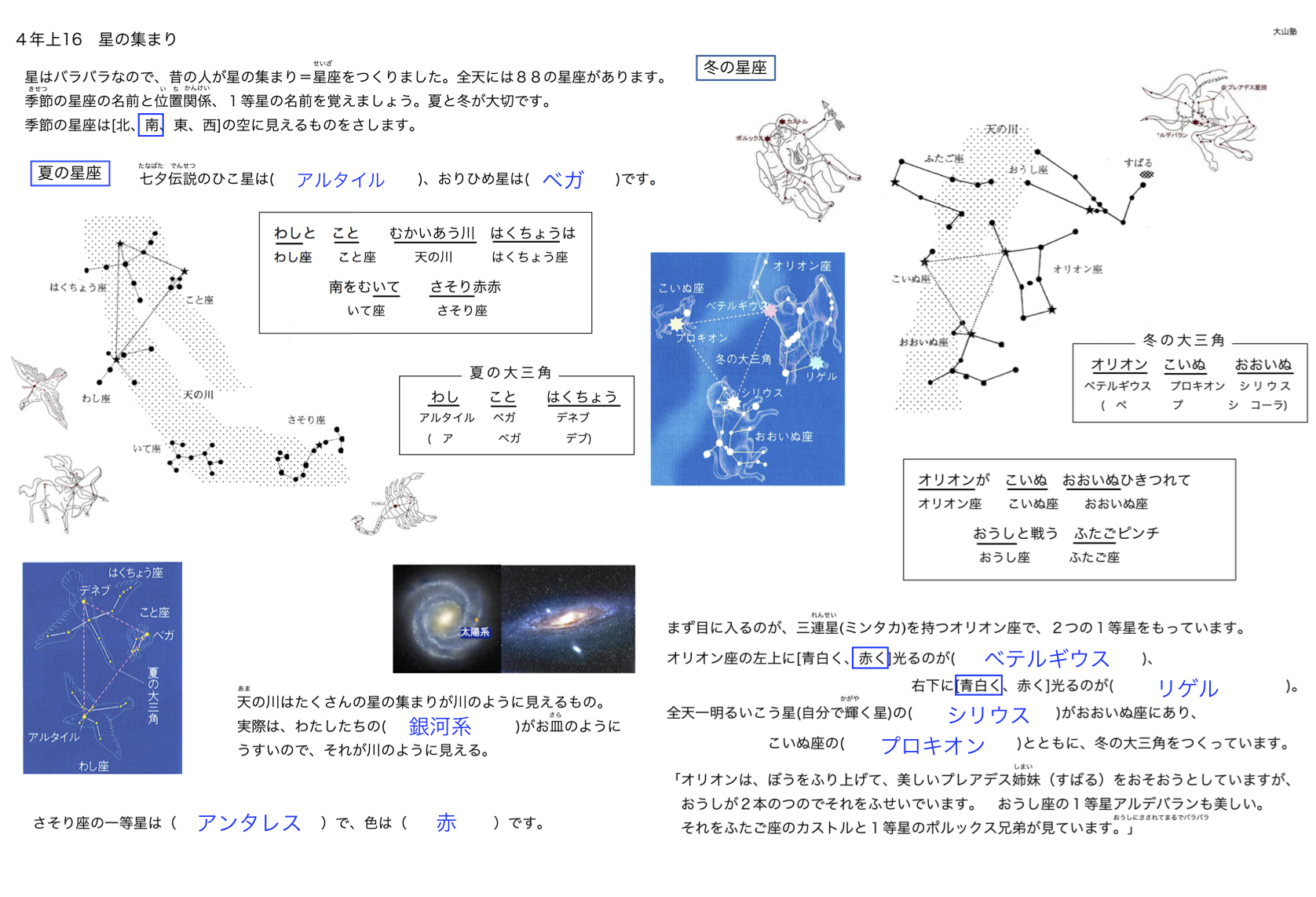
星座の見本

国語の見本


塾で出した漢字の間違いは保存され、忘れた頃に、もう一度テストされます。
できた漢字は消えていき、書けない漢字は入試まで繰り返し出されます。

